日常生活にも役立つ「数字力」を鍛える10分間トレーニング ティーチャー鈴木の数的センスアップ塾 Vol.2

Point-考え方-
「こんな穴あきだらけの虫食い算、本当に解くことができるの?!」と不安になるかもしれませんが、大丈夫!ヒント①の通り、この問題の最大のポイントは「どの順番で数字を埋めていくか」ということです。例えば、最初にHから考えるのはムチャですよね(そもそも、考えるための情報がまったくありませんので…)。何となく解くのではなく、判明している情報をもとに、どの□なら求めることができるかをロジカルに考え、当たりをつけて、順序よく求めていくことが大事です。
さて今回の問題ではどうでしょう?わかっているのは「8」の数字だけに思えますが、□の数(数字の桁数)も立派なヒントです!また、筆算には複数の計算が含まれていて、⑴ABC×D=EFGH、⑵ABC×8=IJK、⑶EFGH+IJK×10=LMNOという3つの計算式に分解することができます。これらの情報を起点に順を追って考えることで道が開けていきます。
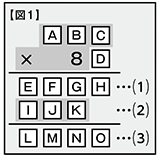
まず注目すべきは、分解した計算式のうち、唯一数字が判明している箇所がある⑵ABC×8=IJKです【図1】。
⑵が3桁となるパターンは限られていて、例えば百の位であるAが2以上だった場合、計算結果は4桁になってしまいます。つまりAには1以外当てはまりません。A=1とわかったので、Iは8か9(B×8で繰り上がりがあった場合)に絞ることができますね。
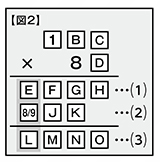
そして、⑵が3桁となるパターンが限られているということは、⑶が4桁になるパターンも限られているということです(⑵が4桁なら⑶は5桁になってしまいますからね)。ですから次に考えるのは、制約の強いE・I・Lの縦列がいいでしょう【図2】。
今わかっている「Iは8または9となる」「Eに0は入らない」「E+Iの計算結果が1桁である」という3つの条件をすべて満たすのは、E=1、I=8、L=9の組み合わせのみですね!
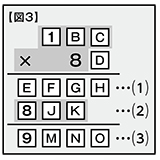
さて、次に注目すべきはどこでしょう?⑵が3桁で百の位が8となるパターンはもっと限られています。A=1とわかっていますから、次はBが攻めやすそうですね【図3】。
では試しにBに数字を入れてみましょう。例えばBが2以上の場合、繰り上がりが発生し、条件に当てはまらないことがわかると思います。つまりBには1しか入りません。
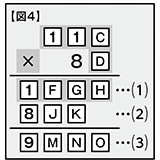
さあ、次です。DとE・F・G・Hの横列に注目してみましょう。AとBが1で、⑴が4桁の数字であることから、実はDを求めることができます【図4】。
試しにDへ数字を入れてみてください。そうするとDが8以下の場合、Cにどんな数を入れようが、⑴は3桁どまりになってしまうことがわかりますね。よって、Dは9と決まるわけです!
では次です。筆算の問題部分で残っているCを攻めていきたいのですが、ここは一筋縄ではいきません。いくつかの場合分けとシミュレーションが必要になってきます。ヒント②はまさしくこの話です。
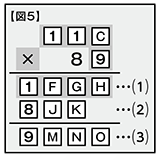
では、どの数字から当てはめていくかですが、コツは極端に小さな数や極端に大きな数から検討すること。まずは⑴から考えましょう【図5】。
C=1の場合、111×9=999となり、計算結果が3桁になってしまうため、これはNG。というわけでCに入る数字は2以上とわかります。
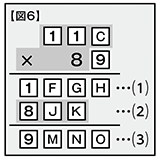
では、Cは2以上であれば何でもOKかというと、答えはノーです。次は⑵を考えます【図6】。
C=9の場合、119×8=952。百の位が8という条件に当てはまらないのでこれはNGですね。同様に、Cに入れる数を8から順番に小さくして計算していくと、Cが3以上のときはすべて⑵の百の位が9になってしまうことがわかると思います。
以上より、Cが確定します。そう、Cは2しか入りません!
ここまでくればゴールは目の前!筆算の問題部分であるAからDまでがすべて決まったので、あとは普通の筆算をしてください。
EFGHは112×9=1008、IJKは112×8=896。LMNOは9968となりますね。
よって、聞かれているNに入る数字は6。これが答えです!
Answer
今回もパズルを通して「ロジカルに考える」ことを経験してもらいました。物事をロジカルに考える際に重要なのは「どの順番で考えるか」。つまり「最も重要なポイントを見極め、最初にそこから攻めていく」ということです。どうしても人間は、一番やりやすそうなことや、最初に思いついたことから始めてしまいがちですが、それでは望む結果を効率的に得ることは難しいでしょう。このような「数学的なものの見方」を養って日常生活やビジネスの場にも役立ててみてくださいね!
小中学生にもおなじみの「虫食い算」ですが、大人も解きごたえのある一問でしたね。 次回は10月号(9/1発刊)掲載予定です。お楽しみに!
[『TACNEWS』 2021年8月号|連載|ティーチャー鈴木の数的センスアップ塾]
筆者 鈴木 伸介(すずき しんすけ)
TAC統計検定®・ビジネス数学検定 ・中小企業診断士講座講師
ハーモニービジョン株式会社代表取締役
各種数学セミナーで講師活動を行いながら、社会人向け数学教室「おとなのENJOY!数学クラブ」「おとな数学オンライン」を主宰、ビジネスパーソンの数学リテラシー向上に尽力している。
保有資格:中小企業診断士・統計調査士・ ビジネス数学検定1級AAA
著 書 : 『もう一度解いてみる入試数学』(すばる舎)
















